Improving quantization by normalizing weights
While trying to implement the previous post about quantization I faced some difficulties. So it is better to write them down for everyone to know (including a future me). Also, I think the process of solving these issues may apply to other problems. Without further do, time to fix🔨!
- Introduction
- Collecting the Dataset
- Visualize the dataset
- Training without PyTorch Model Quantization
- Helper functions for Pytorch Quantizantion and evaluation
- Chain everything together in a single train function
- Experiments
- Conclusion

Introduction
I have hidden all the code from the previous post so we can focus on the experiments but you can find it if you download the notebook or open it in colab.
Remember the model class definition.
class CNN(nn.Module):
def __init__(self, dropout_rate=0.0, norm_w=True):
super(CNN, self).__init__()
self.norm_w = norm_w
# Create the layers normalizing or not the weigths
if self.norm_w:
self.conv_layer1 = nn.utils.weight_norm(nn.Conv2d(in_channels=1, out_channels=32,
kernel_size=3), name='weight')
self.conv_layer2 = nn.utils.weight_norm(nn.Conv2d(32, 64, 3), name='weight')
self.fc = nn.utils.weight_norm(nn.Linear(in_features= 64*5*5, out_features=10), name='weight')
else:
self.conv_layer1 = nn.Conv2d(in_channels=1, out_channels=32,
kernel_size=3)
self.conv_layer2 = nn.Conv2d(32, 64, 3)
self.fc = nn.Linear(in_features= 64*5*5, out_features=10)
# input dimensions are Bx1x28x28 (BxCxHxW)
self.batch_norm1 = nn.BatchNorm2d(32)
self.relu = nn.ReLU()
self.pool = nn.MaxPool2d(kernel_size=2,stride=2)
self.batch_norm2 = nn.BatchNorm2d(64)
self.flat = nn.Flatten()
self.drop = nn.Dropout(p=dropout_rate)
def forward(self, x):
# Block 1
out = self.conv_layer1(x)
out = self.batch_norm1(out)
out = self.relu(out)
out = self.pool(out)
# Block 2
out = self.conv_layer2(out)
out = self.batch_norm2(out)
out = self.relu(out)
out = self.pool(out)
# Flatten the output using BxC*H*W
out = self.flat(out)
out = self.drop(out)
out = self.fc(out)
return out
def add_quant(self):
'''
Returns a new model with added quantization layers
'''
return nn.Sequential(torch.quantization.QuantStub(), self,
torch.quantization.DeQuantStub())
Let's simulate that it is our first time facing this problem, so we haven't thought about normalizing the weights.
model_15, _ = train_model_and_quantize(epochs=15, norm_w=False)
As we can see, the drop in the performance of the quantized model is remarkable. What might have happened? Why the results are way better when using Keras?
We could try training for just 1 epoch and see what happend
model_1, _ = train_model_and_quantize(epochs=1, norm_w=False)
The result of the quantization is better now. What is happening?
The first thing that comes to my mind is taking a look at the weights🔍
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline
def vis_model(model):
w = []
for m in model.modules():
if isinstance(m, (nn.Conv2d, nn.Linear)):
w.extend(np.array(m.weight.data.cpu()).flatten())
plt.hist(w, density=True, bins=128)
plt.ylabel('Ocurrences')
plt.xlabel('Weight')
vis_model(model_15)
vis_model(model_1)
So the weights of the model trained for 15 epochs are larger, may that be what is causing the problem?
We can see how weights are distributed in the Keras model and we will see the wights are smaller (more similar to the model trained for one epoch).
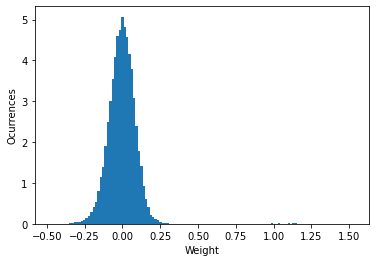
The explanation may be that with larger weights the minimum and the maximum are further apart so the "resolution" of the quantization is worse. One quick fix could be clamping the weights, so they can not be larger or smaller than a certain threshold. But this will make that our model just learn in the few first iterations. It will produce a histogram like this one:

A better option would be normalizing the weights so let's try it.
model_15_norm, _ = train_model_and_quantize(epochs=15, norm_w=True)
We get better results! Lower loss in performance while being able to reduce significantly the size of the model.
And as we can see the weights are now normalized.
vis_model(model_15_norm)
After these experiments, the main takeaways would be the following:
-
We can look at the network's weights and see what is happening. It is a good practice and provides some understanding of how the model is being/has being trained.
-
The values that our weight take are really important in quantization.
-
We have to be careful with the weights not getting too large in our network. As we reward the outputs with higher values is feasible that the model tries to make its weights as big as possible.
-
Normalizing the weight can lead to a better quantized models. Nevertheless, it can increase the training time with the same number of epochs. But it often converges faster, so fewer epochs are needed. You will have to study your problem carefully. No one said it was easy!